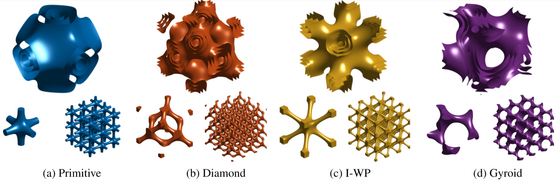
Metamaterials are artificial materials engineered to possess extraordinary physical properties, which are not found in natural materials. In this project, 2D and 3D, uniform and functionally graded mechanical metamaterial architectures are developed with an eye on both static and dynamic applications. Our focus lies on tailorable elasto-mechanical symmetry, high negative/positive Poisson's ratio, ultrahigh strength‐to‐density ratio, negative Cauchy pressure, impact performance and crashworthiness, mechanical wave-filtering and phononic band-gap. Developed single or multiphase lightweight metamaterials may find use in a wide range of applications as, e.g., impact resisting and energy absorbing elements, acoustic dampers, biological tissue scaffolds and meta-implants.

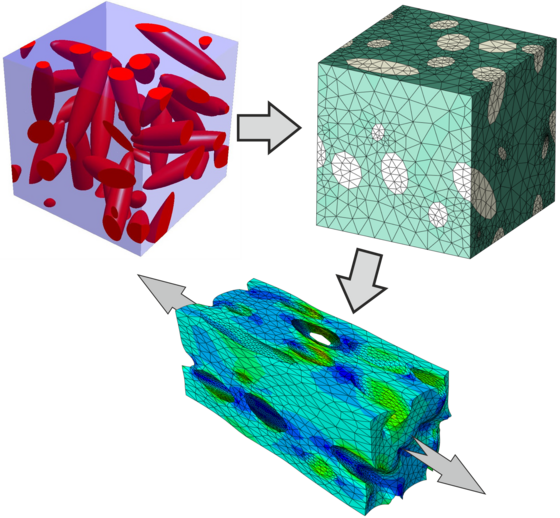
Modern lightweight components are often made of composites. These composites are heterogeneous materials with a distinctive microstructure at a certain length scale. Due to the different constituents and their interactions the materials exhibit superior mechanical properties over the neat materials. To understand the
underlying mechanisms and gain macroscopic responses, state of the art is the utilization of representative volume elements in computational micromechanics.

This project focuses on the generation and discretization of representative volume elements for various types of composites. To capture the statistical nature of the microstructures random generator algorithms are developed. With the use of methods originating from computational geometry different types of inclusions are captured. In the next step, the geometric information is processed into a finite element mesh featuring a periodic mesh topology for the direct application of exact periodic boundary conditions. High quality representative volume elements are then utilized to compute macroscopic responses of complex heterogeneous materials.

Bovine dental enamel exhibits a complicated fibrous hierarchical microstructure and with particular mechanical properties on each size scale. We investigate the mechanical characteristics of enamel. In particular, we study the damage and failure mechanisms on the smallest level of hierarchy.

Sutures, that is soft tissue joining adjacent bone plates, are found in myriad natural protective structures. Their ubiquity suggests an evolutionary convergence to an optimal design for protective structures. The goal of this project is to determine how sutures improve the performance of protective structures and elucidate their structure-function relationship.

Purposeful structuring of layers and interfaces in multi-layer systems containing stiff and brittle materials can lead to structures with exceptional strain relief capabilities. The goal of this project is the computational modeling of highly stretchable multi-layer composites in order to find optimal designs for application in, e.g., stretchable electronics.

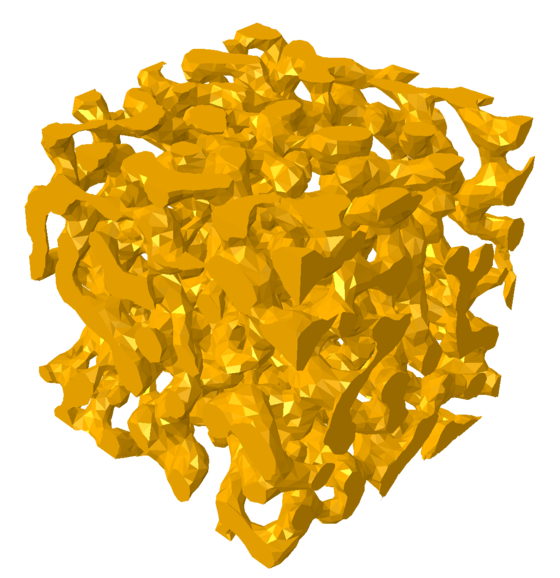
In nanoscale metal-polymer composites such as polymer-filled nanoporous metals, the geometric confinement imposed by the small scale strongly affects the composite's mechanical behavior, resulting in pronounced size effects such as increasing strength with decreasing dimensions. Furthermore, nanocomposites typically exhibit an exceptionally high surface-to-volume ratio that may cause further strengthening and facilitate a functionalization of the material.

In this project, the complex processes involved in the deformation behaviour in nanocomposites are studied. As classical continuum mechanics cannot account for non-local effects or the presence of an interface, extended models need to be developed. These utilize, for instance, gradient extended crystal plasticity or interface elasticity theory to provide valuable insight into mechanisms at the nanoscale and contribute to the design of integrated nanostructured multiphase materials systems and nanoscale smart materials.

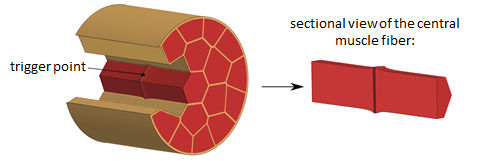
Skeletal muscles are complex fiber-matrix-composites with a hierarchical microstructure. The purpose of this project is to analyze the muscle's mechanical behavior on different hierarchical levels by using finite element simulations.

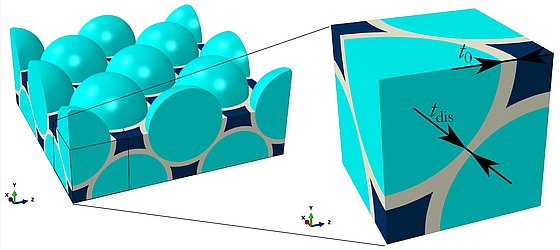
The long-term research goal of the Collaborative Research Center “SFB 986: Tailor-Made Multi-Scale Materials Systems – M3“ is to develop experimental methods for producing and characterizing multi-scale structured materials with tailor-made mechanical, electrical, and photonic characteristics. Within the SFB 986, 20 project leading scientists work on a cross-disciplinary approach to develop completely new types of materials.

In this subproject, the focus is on the modeling and simulation of the non-linear deformation and damage of hierarchical material systems. These materials systems are nano-composites where Fe3O4 or TiO2 ceramic particles are used for reinforcement. Here, conventional continuum mechanic theories are not applicable to describe the corresponding material behavior properly, since the specific architecture and length scale of the microstructure of this nanocomposite is below 100 nm. Overall, the material system is described by four different submodels: ceramics, ligands (interparticle and polymer interactions), interphase and polymer, with each submodel using a different approach. The deformation and damage mechanisms in the hierarchical material systems are investigated by Representative Volume Elements (RVEs). The simulations of these RVEs then provide the basis for the establishment of a non-local macroscopic constitutive law coupled with damage on the next higher hierarchical level.

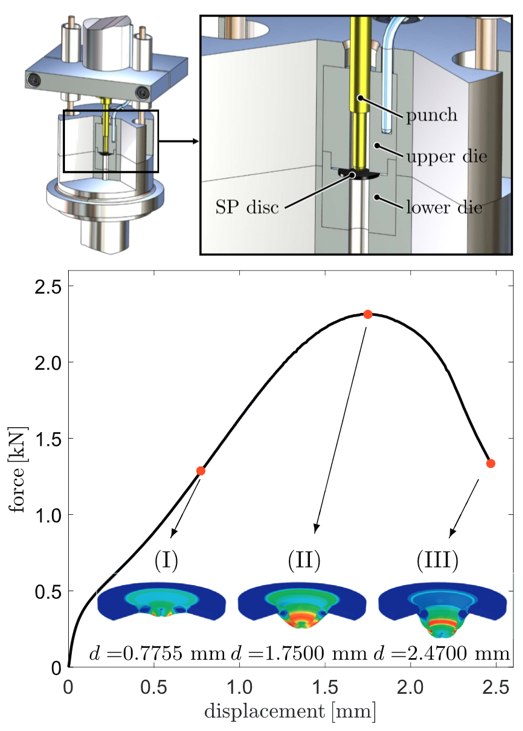
Small punch testing was first developed in the early 1980s for determining the post-irradiation mechanical properties including ductile–brittle transition temperature. The method possesses great advantage over the conventional Charpy test due to the small amount of material needed. Small punch specimens are usually disk-shaped with thicknesses in the range of 0.25-0.5 mm and diameters of 3-10 mm. Therefore, the test is virtually non-destructive, and samples can even be extracted from big components in service.

In this project, through a combined experimental-numerical approach we aim at increasing the accuracy of predictions of materials’ deformation and fracture behavior with the use of small punch testing as the prime mechanical material characterization test. In this context, our project extends from proposing new and pragmatic self-consistent data reduction schemes for determining tensile yield strength of materials to development of finite element method dependent material modeling frameworks for temperature driven ductile–brittle transition.

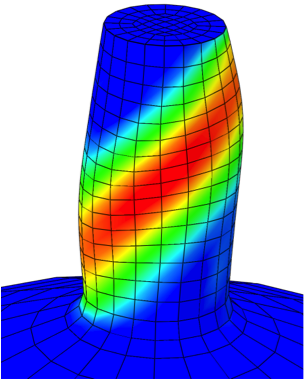
It is well known from numerous experiments that the hardening behavior of polycrystal materials intensifies with decreasing grain size (Hall-Petch effect). The physical reason for this is based on the fact that the amount of grain boundaries, which hinder dislocations to move from one grain to an adjacent grain, is higher in the case of many small grains. Therefore, geometrically necessary dislocations (GNDs) accumulate at grain boundaries and induce an increased resistance to plastic slip. Additionally, strain gradients are induced inside each grain. This is necessary to preserve the geometrical compatibility of adjacent crystals with different orientations joined at the grain boundaries.
The development of GNDs results in additional energy being stored in the material which is modeled by an additional kinematic-like hardening variable, the gradient of plastic slip. Further, latent hardening occurs, i.e., the glide system interaction in form of hardening of inactive slip systems due to active slip systems.

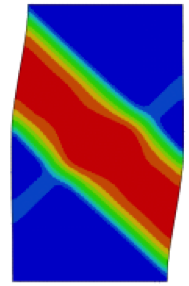
Metallic glass is a solid, amorphous material. It has superb property combinations: high elasticity, high wear and corrosion resistance. Typically metallic glass is hard and brittle. It usually fails by catastrophic shear localization, but some researchers have found that reducing the sample size to sub-micron and nano size can delay the shear localization process and increase the ductility of the metallic glass.
In this project, we model the size-dependent behavior of metallic glasses with continuum mechanics. The problem of classical continuum mechanics is that it does not have a concept of a material length scale. Therefore, it cannot capture size effects. In order to address this problem, we develop a non-local continuum-mechanics based model to qualitatively study the size effects on the shear localization process of metallic glasses.

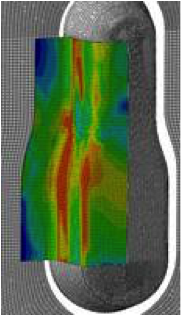
Material modeling is a basic factor in studying metal forming processes. There are different aspects that influence the material behavior during processes including one of the most challenging: the plastic anisotropy. Various phenomena in the elastic-plastic behavior of metals in different loading cases such as Bauschinger effect, anisotropy, strain rate sensitivity and damage need to be accounted for.
In this project, a microstructurally-motivated approach is proposed which accounts for plastic anisotropy, distortional hardening, strain rate sensitivity, Bauschinger effect and kinematic hardening in elastic-plastic behaviour of interstitial free (IF) class of steels. The necessary material parameters in the material model are identified based on the experimental results. The presented material model is applied for several loading cases to investigate its robustness and ability in prediction of material behavior under complex loading conditions. The modeling results are verified by a real forming process.

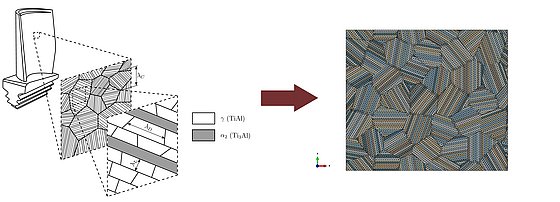
Fully lamellar titanium aluminide (TiAL) alloys exhibit a beneficial combination of good thermomechanical properties with a low density and are therefore increasingly used as structural materials for high temperature lightweight applications like, e.g., low-pressure turbine blades in aircraft engines. Their outstanding macroscopic mechanical properties originate from the lamellar microstructure with its various internal boundaries. This microstructure shows a complex micromechanical behavior, rendering the prediction of the macroscopic materials behavior complicated if not impossible with the use of conventional constitutive material models.

In this project, we set up a temperature-dependent micromechanical constitutive material model which is able to predict the plastic deformation behavior of lamellar TiAl alloys.

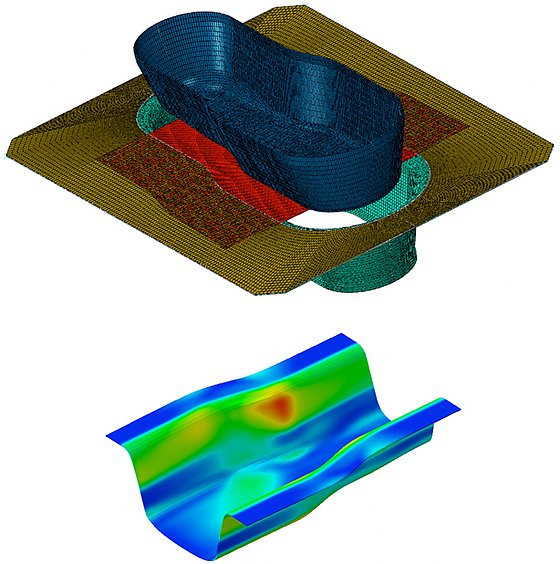
In metallic materials, the localization into deformation bands, as a precursor to fracture, is sourced from two strongly microstructure-dependent constitutive features, (1) path dependence of strain hardening and (2) softening mechanism with, e.g., ductile damage. Here we focus on phenomenological approaches to modeling path dependent hardening and damage considering both experiments and theory.

As path dependent hardening models, Levkovitch--Svendsen cross hardening model and its newly established variants are studied. An increase in material stability and forming limits with decreased local curvature of the yield locus at a loading state with cross hardening is revealed through finite element simulations of stochastic Marciniak-Kuczynski tests and Nakazima tests. The hardening entanglement problem in the original model is remedied by using the radial direction in parallel and orthogonal projections of the fourth-order evolving plastic anisotropy tensor.

Ductile damage driven strain localization and fracture is investigated using shear modified Gurson's porous plasticity model and newly established empirically oriented variants of Lemaitre’s damage model with quasi-unilateral effects and Lode parameter. Thermomechanical coupling as well as nonlocal formulations which incorporates characteristic length scales associated with ductile and brittle damage into the formulation are studied. The models are successfully used in simulation of room temperature fracture development as well as temperature driven ductile-brittle transition in small punch test. Also the implications of the use of proposed model extensions in metal forming practice are discussed.

PUBLICATIONS

Soyarslan, C., Bargmann, S.
Thermomechanical formulation of ductile damage coupled to nonlinear isotropic hardening and multiplicative viscoplasticity
Journal of the Mechanics and Physics of Solids, Vol. 91, Pages 334--358, 2016.

Soyarslan, C., Klusemann, B.; Bargmann, S.
A directional modification of the Levkovitch-Svendsen cross-hardening model based on the stress deviator
Mechanics of Materials, Vol. 86, Pages 21--30, 2015.

Soyarslan, C., Türtük, I., Deliktas, B., Bargmann, S.
A thermodynamically consistent constitutive theory for modeling micro-void and/or micro-crack driven failure in metals at finite strains
International Journal of Applied Mechanics, Vol. 8, No. 1, 1650009 (20 pages), 2016.

Behrouzi, A., Soyarslan, C., Klusemann, B., Bargmann, S.
Inherent and induced anisotropic Finite visco-plasticity with applications to the forming of DC06 sheets
International Journal of Mechanical Sciences, Vol. 89, Pages 101--111, 2014.

Soyarslan, C., Klusemann, B., Bargmann, S.
The effect of yield surface curvature change by cross hardening on forming limit diagrams of sheets
International Journal of Mechanical Sciences, Vol. 117, Pages 53--66, 2016.

Soyarslan, C., Richter, H., Bargmann, S.
Variants of Lemaitre's damage model and their use in formability prediction of metallic materials
Mechanics of Materials, Vol. 92, Pages 58--79, 2016.

Soyarslan, C., Richter, H., Bargmann, S.
Lode Parameter Dependence and Quasi-Unilateral Effects in Continuum Damage Mechanics: Models and Applications in Metal Forming
Key Engineering Materials 651, 187-192, 2015.

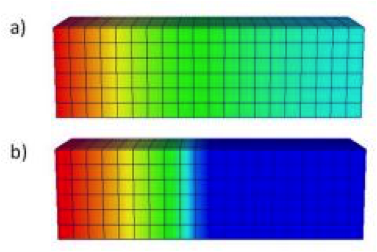
In glassy polymers, diffusion of vapours and liquids deviates significantly from classical Fickian behaviour. An important type of anomalous diffusion is Case II diffusion, a process characterized especially by wave-like penetrant propagation with a sharp wave front. Pressure exerted by the penetrating solvent enforces a rearrangement of the polymer network and thus a transition from the glassy to a rubbery state. Concurrently, the rate of rearrangement inhibts the solvent uptake, thus causing formation of the characteristic front.
Evidently, diffusion and deformation are strongly coupled for Case II diffusion. To describe the process within the framework of continuum mechanics, the equations governing Case II behaviour are derived from fundamental balance principles, leading to thermodynamically consistent relations. The formulation incorporates diffusional, inelastic and thermal effects and elucidates the nature of the coupling between the various fields.

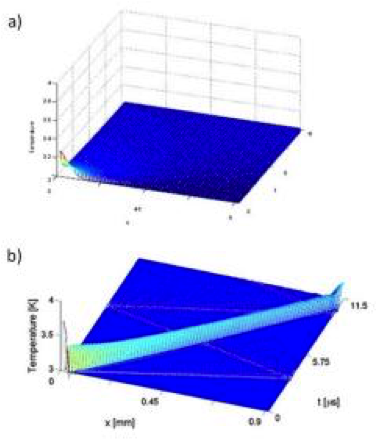
Thermoelasticity represents the fusion of the fields of heat conduction and elasticity in solids and is usually characterized by a twofold coupling. Usually, heat conduction in solids is based on Fourier’s law which describes a diffusive process. However, it is not capable of modeling the phenomenon of second sound which occures at cryogenic temperatures. The Green-Naghdi model makes use of the notion of thermal displacement and allows for heat waves and is at variance with the standard Fourier theory. It has attracted considerable interest, and has been applied in a number of disparate physical circumstances; here, the second sound phenomenon.

The main goal of the project is the investigation of the overall behavior of materials containing nano-particles and/or nano-pores and having a stochastic structure. A statistical method – the method of conditional moment functions – will be generalized to take into account the surface stress effect at the nano-scale. A Gurtin-Murdoch interface model will be used to describe the stress discontinuity on the surface of matrix/nano-particles. Tensor operators given on the surface will be applied to stress concentration problems in composites for investigation of the local stress-strain state on the interface between matrix and nano-particles or nano-pores.